疲劳寿命为何总是‘测不准’？

在材料或构件的疲劳测试中，即使控制工况（如应力水平、环境温度、加载频率）完全一致，疲劳寿命数据仍普遍存在显著分散性——这源于材料内部缺陷（如夹杂、晶界差异）、试样加工误差、测试系统波动等多因素的随机影响。

这种分散性导致疲劳寿命无法通过单一数据直接精准预测，因此必须引入统计学方法，建立“寿命-概率-置信度”的关联模型，才能实现保守且可靠的疲劳分析，满足工程设计对安全性的要求。

首先，对于试验得到的同一工况下的疲劳数据是符合正态分布的。对于正态分布，用以下公式描述，即

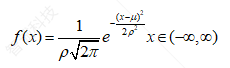
(1.1)

式中，μ为平均值，ρ为标准差。

我们知道正态分布是由两个参数μ与ρ确定的。对于任意一个服从N (μ,ρ2)分布的随机变量X，经过下面的变换以后都可以转化为μ=0,ρ=1的标准正态分布。转换公式为:

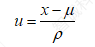
(1.2)

标准正态分布概率密度函数为

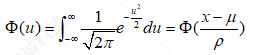
(1.3)

疲劳统计分析的任务是要回答:在给定的应力水平下，寿命为N时的失效概率Pf或存活概率Ps是多少?或者说,在给定的失效概率Pf或存活概率Ps下的寿命N是多少?

我们定义样本的平均值为

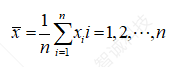
(1.4)

方差为

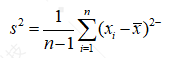
(1.5)

通过对式（1.2）进行转换，我们可以得到与失效概率Pf对应的对数疲劳寿命xp为

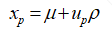
(1.6)

我们用样本均值与标准差替代式（1.6）的对应部分，可得

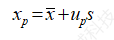
(1.7)

但是，替换为样本的均值和标准差会导致概率问题，因为样本并不能完整体现整体，安全寿命的失效概率P是针对样本中的个体而言的。直接使用样本的均值和标准差，其置信度为50%。若想提高置信度，需要通过t分布或者卡方分布对样本相对于整体的概率进行统计。

我们现在已知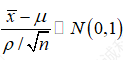，若想对疲劳寿命的估计更加保守则需要将μ的值估计得小一点。假设我们现在想要获得置信度为

的概率，可以记作

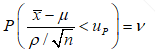
(1.8)

将式（1.8）中的不等式进行移相，可得

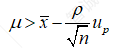
(1.9)

我们既要保守估计，就是将μ取最小值，此时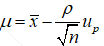。但式（1.6）中的ρ依旧是属于总体的标准差，我们还需要通过t分布建立总体与样本间的关系，t分布的概率密度函数为

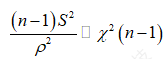
(1.10)

由于t分布是对右侧进行统计，所以我们需要将ρ取最大值，与式（1.8）一样，我们将t分布记作

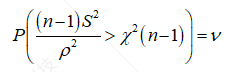
(1.11)

将式（1.11）中的不等式进行移相，可得

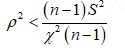
(1.12)

我们对ρ取最大值，此时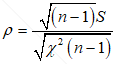。至此，我们已经将总体和样本的均值和标准差建立了关系，将其代会式（1.6）整理可得

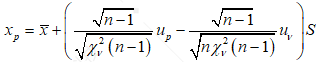
(1.13)

式中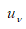，,是与置信度v相关的标准正态分布变量的值,可由正态分布函数表查得。我们还可以将式（1.13）简写为

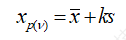
(1.14)

式中k称为单侧容积系数，可以根据下式确定

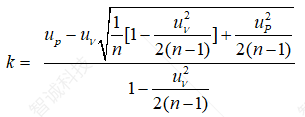
(1.15)

据此，才能有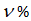的把握说，在该应力水平下，至少有PS%的疲劳寿命大于N。